「私の論文」
上記論文は１９５６年マーカスが３３歳の時に初めて極性溶媒中の分子間電子移動（外圏型電子移動）の理論を発表した時のもので、その後このシリーズは続けられるが、いわゆる“マーカス理論”の骨格はこの論文でできあがっている。この理論が発表された当時学会の受け止め方は複雑であった。あまりにも斬新過ぎて理解できない人が多く、またすぐには実験的な裏付けが見つからなかった。そんなわけでマーカス理論は関心をもたれながらも評価が定まらず、その後いくつもの関門を経てようやく実験的に確認され、１９９２年にノーベル化学賞を受賞するようになる。その経緯をここで紹介する。それはスリルのある物語で、そのような科学研究のソサイエティに接していた私も大いに楽しむことができた。
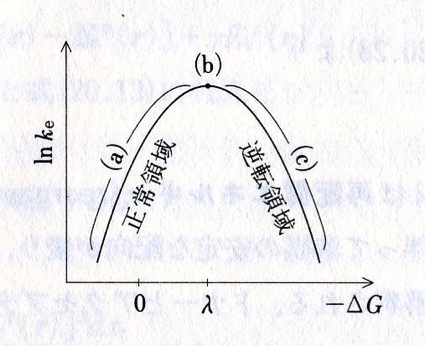
上図はマーカスのパラボラあるいはマーカスのエネルギーギャップ則である。ここで
は電子移動速度である。
は自由エネルギーギャップあるいはdriving forceといい、電子移動前の状態(始状態)の自由エネルギーから電子移動後の状態（終状態）の自由エネルギーを差し引いたものである。lnがに対して上に凸のパラボラになるのが特徴である。頂点(b)は
のときで、
は電子移動に伴う溶媒の再配置エネルギーである。マーカス理論では 
と書かれる。ここで
はボルツマン定数、Ｔは温度である。
は当初衝突頻度と呼ばれたが、反応分子間の電子トンネルに関する電子雲の重なりに関係している電子因子である。指数関数の部分は溶媒分子配向に関係するので核因子と呼ばれる。マーカスのエネルギーギャップ則は核因子に関するものである。
マーカスのエネルギーキャップ側では、がより小さい時はlnはの増大とともにパラボラ的に増大し、正常領域(a)と呼ばれる。それは当時までに、通常の化学反応（置換・付加など）においては速度がの増大とともに増加することはわかっており、その傾向がマーカス理論のこの領域で似ているために正常と呼ばれた。また、がより大きい時はlnはの増大とともにパラボラ的に減少し、逆転領域(c)または異常領域と呼ばれる。後者の名前は当時までにそのような傾向を示す化学反応の例がほとんど報告されていなかったからである。また、正常領域においても、それまでに見出されていた経験則（たとえば、ブレーンステッド触媒則、ハメット則、堀内―ポラニ則など）ではln
はと共に線形に増大することがわかっており、自由エネルギー直線関係の法則といわれていた。このように経験則にことごとく反するために、マーカス理論は実験の裏付けがない理論であった。
しかしマーカスが電子移動速度には溶媒の運動が大きく関与していることを示したのは大いに注目された。その当時まで、化学反応速度を決めるのは主に反応体に含まれる官能基の働きであり溶媒は補助的な役割しか果たさないと考えられていた。それに対してマーカスは電子移動反応（酸化・還元）が他の化学反応と異なる機構（電子トンネル効果）で起こっているために溶媒が主要な役割を果たすことを示したのである。そのしくみはおよそ次のとおりである。電子移動反応はドナー分子とアクセプター分子（両者を合わせて反応体と呼ぶ）間の相互作用が弱く、電子トンネル効果を通じてかろうじて起こる現象である。電子トンネル現象がおこるためには始状態と終状態のエネルギーが等しく（バランスするように）ならなければならない。しかるにほとんどの反応体で始状態と終状態の平衡状態にある自由エネルギーは互いに異なっている。そのため分子環境（溶媒分子）が揺らいで非平衡状態をとることによって、始状態と終状態のエネルギーが等しくなる瞬間を待たなければいけない。その瞬間がどれほど多く実現されるかによって反応速度が決まるのである。幸いなことに、始状態と終状態で反応体内の電荷分布が大きく変わるので、反応に伴う反応体と極性溶媒の相互作用エネルギーの変化が大きい。そこで溶媒の配向が揺らぐことによって、始状態と終状態のエネルギーのバランスを容易にとることが出来るようになるのである。
それではマーカス理論で何故パラボラのエネルギーギャップ則が得られたのであろうか。マーカスは電場に比例して分極の大きさが決まるという線形応答近似を使った。そして非平衡電磁力学と変分法を組み合わせるなど高度な理論技術を駆使して、始状態と終状態の微細状態のエネルギーが等しくなるすべての場合を数え上げ、電子移動速度を導いた。そこでは溶媒の場のエネルギーが各場所の溶媒の分極の２乗に比例するという性質が使われており、その結果マーカスのパラボラになったのである。また溶媒の再配置エネルギーを誘電率と屈折率を用いて定式化した。
フラッシュ・フォトリシスの実験技術などが進展するにつれて、マーカス理論を実験的に検証する動きが強まってくる。その中で最も有名な実験が１９７０年にレームとヴェラ―によってなされた。種々の蛍光体と消光体の組み合わせにたいして、消光速度
をはかり、そこから電子移動速度をもとめる実験である。結果を下図に示す。
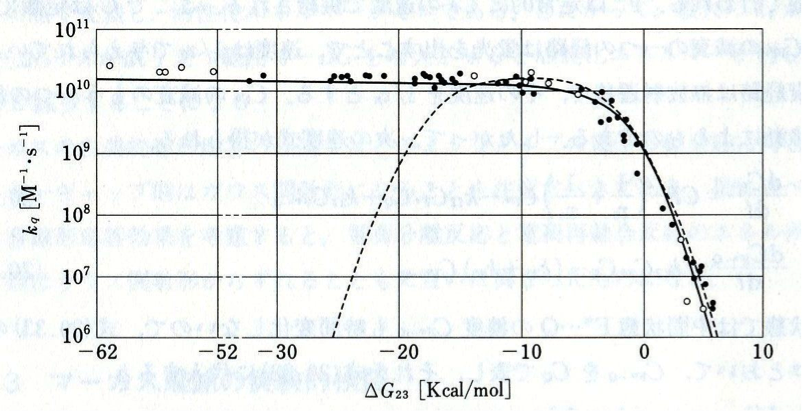
ここでエネルギーギャップの負の値を横軸にしているため、右側に正常領域が見られる。実験データは黒丸や白丸でプロットされており、エネルギーギャップが大きくなるにつれて速度は一定になり、逆転領域が見られない。点線はマーカスのエネルギーギャップ則を正常領域で一致するように描いたものである。このように逆転領域で理論と実験の不一致が顕著になるために、マーカス理論は窮地に立たされることになる。
その後このレーム・ヴェラーの実験の解釈をめぐってさまざまな議論がかわされる。エネルギーギャップの大きな領域で速度が一定になるのは拡散律則（溶液中をドナーとアクセプターが拡散して衝突する速度より反応が早い時拡散速度が観測される）によるのだという説、それにしても６０Kcal/molの大きなエネルギーギャップまで拡散律則というのはおかしいという説、大きなエネルギーギャップ領域では反応体の励起状態が終状態になっているため実質のエネルギーギャップはもっと小さいという説などが提案された。また溶媒揺らぎだけではなく反応体の分子振動の量子効果が効いているという説も出された。この理論はジョルトナーらによって提出され、分子振動の量子効果によって逆転領域のパラボラ的減少は軽減されることが示された。一方溶液中のドナーとアクセプターに距離分布があって、それぞれのペアーごとに電子因子の値や再配置エネルギーの値が異なり、全体としてそれらの値が広範に分布することによってエネルギーギャップ則の幅が広がり、逆転領域が表れにくくなることも示された。
このような議論がおこっているとき、私と又賀先生は新しい電子移動理論を提案した。電子移動反応では始状態か終状態、あるいは両状態で必ず反応体に正か負の電荷が現れる。電荷に接する極性分子は強い電場を受け、強く配向し溶媒として強く分極する。そのとき電場の強さに比例して分極するという線形応答の近似はなりたたない。これを非線形性あるいは誘電飽和という。そのような非線形性をあらわに考慮して計算すると、エネルギーギャップ則は次の２種類の電子移動反応に対して異なる形状になる。光誘起電荷分離反応
ではエネルギーギャップ則のピークの位置が変わらずに、鍋型に変形し幅が増大する。電荷再結合反応
ではエネルギーギャップ則のピークの位置がエネルギーギャップの小さい方向にシフトし、ピークが先鋭化し幅が縮小する。その結果、光誘起電荷分離反応では逆転領域が現れにくくなり、レーム・ヴェラ―の実験はそれを表わしているのであろうという推測を行った。他方電荷再結合反応では逆転領域が見やすくなると予測され、後に又賀の実験でそれが示された。
非線形性の問題は、マーカス理論で避けて通った問題であったため、私たちの提案は多方面で検討がなされるようになった。私たちも分子動力学シミュレーションを実行して、電荷を持つ分子の周りの極性溶媒分子の配向を詳しく調べた。その結果予想通り、電荷を持つ分子に接する１層目の溶媒分子は強く配向し、誘電飽和に近い状態であった。しかし２層目、３層目と外に向かうにつれ溶媒分子の分極の非線形性は次第に弱くなった。シミュレーションの結果を用いて光誘起電荷分離反応のエネルギーギャップ則を求めるとエネルギーギャップ則はパラボラよりいくらか鍋型になって幅が広くなるが、マーカス理論の予言するエネルギーギャップ則と大きく変わることはなかった。このことは統計力学的に次の知見を与えている。荷電分子の周りの強い極性電場に対して直近の溶媒分子は誘電飽和を起こすほどに強く非線形分極しているが、その分子数は数個に限られる。誘電飽和層の外側はほとんど誘電飽和しないで、ほぼ線形分極する分子が多数取り巻いており、その数は十数個に及ぶ。両層の分子数の違いによって、非線形分極応答の効果が薄められ、近似的に線形理論が成り立つようにふるまってしまう。すなわち電子移動反応に直接関与する溶媒分子の数が非常に多いためにほとんど線形応答が成り立ってしまうのである。ここにおいても線形応答理論のしぶとさが表れる。かくして自然現象はシンプルに表現される。
以上の百科繚乱の議論が行われる中で、マーカス理論を検証する有力な課題が浮き彫りになった。マーカス理論では反応体が衝突錯体を形成してから電子移動が起こると仮定し、電子因子を一定とした。しかし電子移動は実際には衝突錯体を形成せずとも、いろいろな反応体間の距離から多かれ少なかれ起こる。これは通常の化学反応と異なる点である。そこで電子因子を一定にするような分子系を作れば、核因子であるマーカスのエネルギーギャップ則そのものを検証することが出来るはずである。それを１９８４年にミラーは下図に示すような分子系を化学合成して実行した。変形しにくいステロイド分子（スぺーサーＳ）の両端にドナー分子（Ｄ）とアクセプター分子を共有結合で固定し（Ｄ－Ｓ－Ａ分子系を作り）、ドナーとアクセプター間の距離が動かないようにした。またアクセプター分子をいろいろ置き換えて何種類ものＤ－Ｓ－Ａ分子系を用意した。そのすべての分子系でドナーとアクセプター間の距離(edge to edge)を同じにした。この場合ドナーはパルスラジオリシスで生成したビフェニル・アニオンラジカルであり、アクセプターは種々の酸化還元電位を持つ共役分子である。
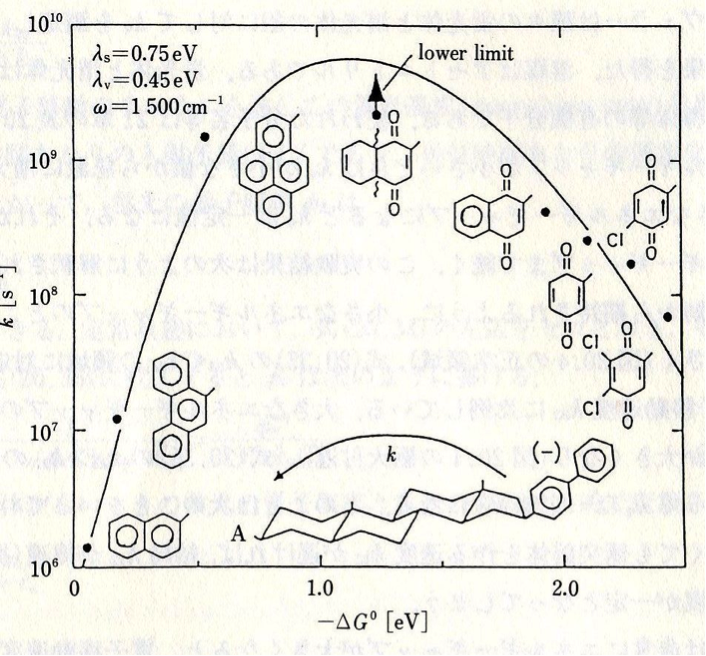
実験結果は黒丸で示されており、明確な逆転領域が見られる。実線は溶媒分子の揺らぎと分子内振動を同時に考慮したジョルトナーの理論を使って求めたものである。理論曲線と実験データとの一致は極めて優れている。
と
はそれぞれ溶媒の再配置エネルギー、分子振動の再配置エネルギーを示し、その大きさはそれぞれの電子移動反応への寄与の大きさを表す。溶媒の寄与の方が分子振動の寄与より大きいことが分かる。それでも逆転領域で減少が緩和されているのは分子振動の量子効果の表れである。ジョルトナーの理論はマーカスの理論を下敷きにして、分子内振動の寄与を追加し拡張した理論である。
このミラーの実験によってマーカス理論はゆるぎない実験的確証を得ることになる。電子移動反応機構の物理的明快さとその応用範囲の多様性故に、電子移動反応の解明にかかわった研究者に近いうちにノーベル賞が与えられるであろうと多くの人々が期待と興奮に包まれた。しかしながら、ここに思いがけないことがおこる。ドイツのミヒェルとフーバーとダイゼンホーファーが１９８５年に紅色光合成細菌Rhodopseudomonas viridisの反応中心のＸ線構造解析を成功させてしまう。このような大きな蛋白質複合体の構造が明らかになったことは驚異であるばかりでなく、光合成初期過程の研究に計り知れない影響を与えることがすぐに読み取れた。そして３人はわずか３年後の１９８８年にノーベル化学賞を授けられる。これにより電子移動研究のソサイエティは電子移動で早期にノーベル賞を受賞するテャンスを失い残念に思われたが、反応中心の構造解析の重要性を考えると、この異例の早期のノーベル賞受賞は妥当であると言わざるを得なかった。
電子移動分野の研究はその後も発展し続ける。特にピコ秒・フェムト秒分光の技術を駆使して、高速の電子移動反応を研究できるようになった。電子移動速度が溶媒緩和速度より早く進み振動緩和速度より遅い場合や、電子移動速度が振動緩和速度と同じかそれより早い場合には、溶媒のダイナミクスや振動のダイナミクスが関与した新しい反応過程が見られる。これらに対して、実験的にはフレミングが指導力を発揮し、理論的には住とマーカスが新しいダイナミクスの理論を提出した。またベラタンとオヌチックは蛋白質中電子トンネル経路についていろいろな解析を行い、ドナーとアクセプター間を最短のボンドで伝っていくpathway modelが有効であることを示した。
一方、タンパク質中電子移動で蛋白質のような決められた構造を持つ媒体が極性溶媒と同じような分極効果を持ち得るのかが調べられた。ダットンらは紅色光合成細菌Rb. sphaeroidesの
サイトのキノンを種々の酸化還元電位をもつキノン類に置換し、それぞれに対して
の電子移動速度を測定した。得られたエネルギーギャップ則で正常領域の存在を確認したが、逆転領域のデータが不足した。伊藤（繁）らはほうれん草のPSIのフィロキノンを種々の酸化還元電位を持つキノン類で置換し、それぞれに対して
の電子移動速度を測定した。得られたエネルギーギャップ則で正常領域と逆転領域の存在を確認することができた。実験データの解析から蛋白媒質のと分子振動のは同程度の大きさで比較的小さな値であることがわかった。ダットンの調べた紅色光合成細菌のは非常に大きくは小さいと予想された。このように構造を保持する蛋白質媒体であってもその構造の揺らぎによって電子移動を引き起こすことは十分可能であることが示された。
電子移動の研究がさまざまな分野に拡張して発展していく中で、化学の分野でノーベル賞受賞が一巡し、１９９２年ようやく電子移動分野でノーベル化学賞が授けられた。受賞者はマーカス単独である。今や電子移動は極めて多くの研究者で進められており、どの３人に絞られるか注目されていたのであるが、たとえばミラーやジョルトナーやフレミングやダットンや又賀なども含められるかと思われたのであるが、マーカス単独受賞となった。私はこの電子移動研究を回顧する文章を書いてみて、マーカスの単独受賞が正しい選択だったとわかる。マーカスは１９５６年からずっと電子移動研究のソサイエティの中心にいたのである。私も”マーカスのパラボラ“という魔物に引き込まれた一人だった。
ところでレームとヴェラ―の逆転領域が見られない実験結果の解釈はどうなったのであろうか。多分非常に大きなエネルギーギャップ領域では反応体の励起状態が終状態になっているため実質のエネルギーギャップはもっと小さいという説が今では有力なのではないかと思われる。それほど大きくないエネルギーギャップ領域ではドナーとアクセプターの距離分布が影響しているように思われる。
